本文共 2030 字,大约阅读时间需要 6 分钟。
一、机器学习方法:拟合预测曲线
我们可以使用机器学习来挖掘它们之间的关系(见下图的「最佳拟合预测曲线」),即给定一个不属于数据点的特征值,我们可以准确地预测出输出(特征值和预测线的交点)。
选择一个模型
(1)模型种类
1、线性模型
2、指数模型
为了使用机器学习来做预测,我们需要选择一个能够拟合收集到的数据的最佳模型。
我们可以选择一个线性(直线)模型,并通过改变其陡度/梯度和位置对其进行调整,从而匹配数据点。
我们也可以选择一个指数(曲线)模型,并通过改变其曲率(curvature)和位置对其进行调整,从而匹配同一数据点集。
(2)成本函数
为了比较哪个模型拟合得更严密,数学上我们将最佳拟合定义为一个需要被最小化的成本函数。 成本函数的一个简单样例是每个数据点所代表的实际输出与预测输出之间偏差的绝对值总和(实际结果到最佳拟合曲线的垂直投影)。用图表表示,成本函数被描述为下表中蓝色线段的长度和。

注意:更准确地说,成本函数往往是实际输出和预测输出之间的方差,因为差值有时是负数;这也称为最小二乘法。
(3)线性模型简介
线性模型的数学表示是:y=w*x+b
- 调整 W 来改变线性模型的斜率

通过使用许多个 W、b 的值,最终我们可以找到一个最佳拟合线性模型,能够将成本函数降到最小。
- 调整 b 来改变线性模型的位置

问题来了:除了随机尝试不同的值,有没有一个更好的方法来快速找到 W、b 的值?
(4)梯度下降
- 梯度下降法的基本思想可以类比为一个下山的过程。
- 假设这样一个场景:一个人被困在山上,需要从山上下来(i.e. 找到山的最低点,也就是山谷)。但此时山上的浓雾很大,导致可视度很低。因此,下山的路径就无法确定,他必须利用自己周围的信息去找到下山的路径。这个时候,他就可以利用梯度下降算法来帮助自己下山。
- 具体来说就是,以他当前的所处的位置为基准,寻找这个位置最陡峭的地方,然后朝着山的高度下降的地方走,然后每走一段距离,都反复采用同一个方法,最后就能成功的抵达山谷。
- 同理,如果我们的目标是上山,也就是爬到山顶,那么此时应该是朝着最陡峭的方向往上走。
- 梯度下降的基本过程就和下山的场景很类似。
- 首先,我们有一个可微分的函数。这个函数就代表着一座山。
- 我们的目标就是找到这个函数的最小值,也就是山底。
- 根据之前的场景假设,最快的下山的方式就是找到当前位置最陡峭的方向,然后沿着此方向向下走,对应到函数中,就是找到给定点的梯度 ,然后朝着梯度相反的方向,就能让函数值下降的最快!因为梯度的方向就是函数之变化最快的方向。
- 所以,重复利用这个方法,反复求取梯度,最后就能到达局部的最小值,这就类似于我们下山的过程。(局部因为每次都选择最陡峭的不一定就到了最低点,可能是次低点)
二、基础数学知识
1、微分(求导)
- 看待微分的意义,可以有不同的角度,最常用的两种是:
- 函数图像中,某点的切线的斜率
- 函数的变化率

2、梯度 gradient(多元函数分别求偏导,有方向)
- 梯度实际上就是多变量微分的一般化。
- 梯度就是分别对每个变量进行微分,然后用逗号分割开。
- 梯度是用<>包括起来,说明梯度其实一个向量。
梯度的意义
- 在单变量的函数中,梯度其实就是函数的微分,代表着函数在某个给定点的切线的斜率。
- 在多变量函数中,梯度是一个向量,向量有方向,梯度的方向就指出了函数在给定点的上升最快的方向。
- 梯度的方向是函数在给定点上升最快的方向,那么梯度的反方向就是函数在给定点下降最快的方向,这正是我们所需要的。所以我们只要沿着梯度的方向一直走,就能走到局部的最低点!
3、梯度下降算法
- Step 1:在当前位置以最陡的下降梯度确定方向
- Step 2:在该方向上采取步长 X
- 重复&更新
4、梯度下降算法的实例
(1)单变量函数的梯度下降
- 假设有一个单变量的函数
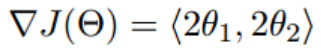
- 函数的微分
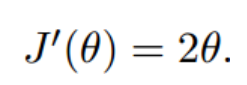
- 初始化起点为
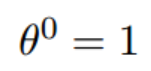
- 学习率为
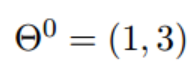
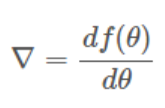
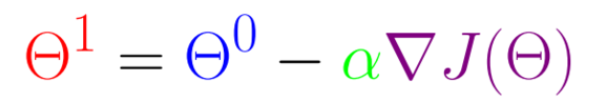
(1.2)梯度下降的迭代计算过程
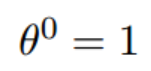
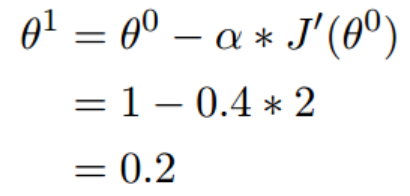
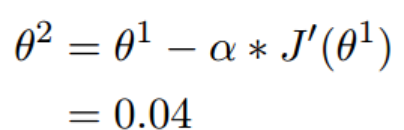
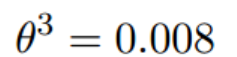
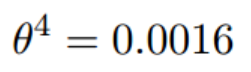

经过四次的运算,也就是走了四步,基本就抵达了函数的最低点,也就是山底
(2)多变量函数的梯度下降
- 假设有一个双变量的函数
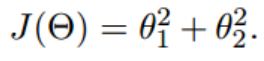
- 假设初始的起点为
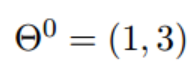
- 初始的学习率为
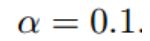
- 函数的梯度为
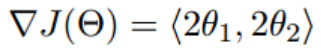
现在要通过梯度下降法计算这个函数的最小值。我们通过观察就能发现最小值其实就是 (0,0)点。但是接下来,我们会从梯度下降算法开始一步步计算到这个最小值!
(2.1)梯度下降的迭代计算过程


经过100次迭代后,已经基本靠近函数的最小值点(0,0)
七、梯度下降仅能得到局部最优解
- 梯度下降的三要素:
- 起始点(初值)
- 梯度
- 步长(学习率)

- 下山场景与梯度下降
- 下山的人实际上就代表了反向传播算法
- 下山的路径其实就代表着算法中一直在寻找的参数Θ
- 山上当前点的最陡峭的方向实际上就是代价函数在这一点的梯度方向
- 场景中观测最陡峭方向所用的工具就是微分
- 在下一次观测之前的时间就是有我们算法中的学习率α所定义的。
TODO:使用梯度下降法最小化成本函数以得到最优的W和b
转载地址:http://xffr.baihongyu.com/